Lab 6b: Closed-loop Process Control
Download This Document
1. Objectives
- Generate PWM outputs to implement analog motor supply voltage.
- Implement a tachometer operation using PIC32 Timers.
- Develop MPLAB X projects that implement closed-loop motor control.
- Develop the C program code to implement a PI controller and a moving averaging digital filter.
- Manage multiple background tasks in an interrupt driven system.
- Send real-time data to monitoring devices.
2. Basic Knowledge
- Fundamental knowledge of linear systems.
- How to configure IO pins on a Microchip® PIC32 PPS microprocessor.
- How to implement a real-time system using preemptive foreground-background task control.
- How to generate a PWM output with the PIC32 processor.
- How to configure the Analog Discovery 2 to display logic traces.
- How to implement the design process for embedded processor based systems.
3. Equipment List
3.1. Hardware
- Workstation computer running Windows 10 or higher, MAC OS, or Linux
In addition, we suggest the following instruments:
3.2. Software:
The following programs must be installed on your development workstation:
- WaveForms (if using the Analog Discovery 2)
- Spreadsheet application (such as Microsoft Excel)
4. Project Takeaways
- How to read an analog voltage with a PIC32 processor.
- How to use the PIC32 Output Compare to implement a PWM analog output.
- How to use the PIC32 Timer external input to measure frequency to implement a tachometer.
- How to use the PIC32 Input Capture period measurement to implement a tachometer.
- Fundamental analog and filtering concepts for data smoothing and closed-loop control.
5. Fundamental Concepts
The purpose of this laboratory exercise is to implement a closed-loop control system to control the speed on a DC electric motor. The processing involves two different types of analog inputs and generating an analog output using pulse-width modulation. We will see how both analog and digital signal conditioning can reduce measurement noise that can degrade system performance. This lab requires that an electronic circuit be constructed to provide an interface between the Basys MX3 board and the DC motor tachometer.
5.1. Feedback Control
Feedback control is a common and powerful tool when designing a control system that can compensate for load variations and perturbations. A feedback loop as portrayed in Fig. 5.1, taking the system output into consideration. This enables the system to adjust its performance to meet a desired output response in spite of variations in motor characteristics, noise, and disturbances that may be introduced anywhere in the system.
The controller action and feedback compensation is implemented using digital filtering and digital control theory. Digital filtering involves discrete time and discrete amplitude signals that are generated when continuous signals are sampled with an analog-to-digital converter at fixed time intervals.1) The primary objective of the control system is to achieve zero error, designated as “$e_n$” in Fig. 5.1. The error signal is the difference between the sum of the control inputs, $r_n$, and the feedback signal, $y_n$. The variable $c_n$ is the output from the control algorithm used to drive the system machine or process. The subscript “n” on these variable denotes the fact that they are generated at discrete times.
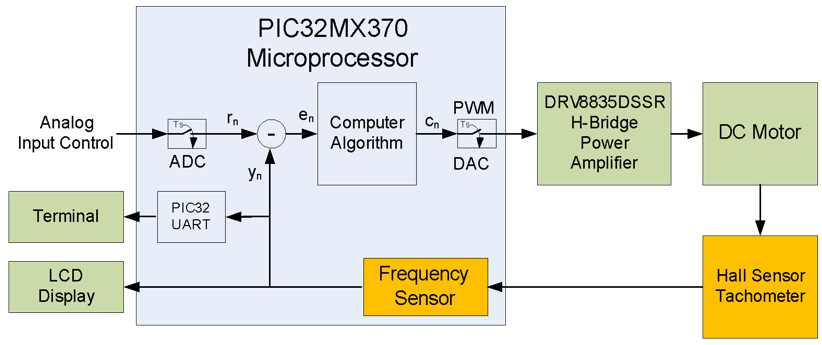 Figure 5.1. Closed-loop motor control block diagram.
Figure 5.1. Closed-loop motor control block diagram.
Besides changes in mechanical loads on the motor, the major sources of noise or disturbances into the control loop is from the output amplifier, the process converting electrical energy to mechanical energy, and the tachometer used to measure the mechanical output. Noise can also be introduced on both the analog and discrete inputs. In our system we will consider only disturbed signals at the output of the tachometer and the output of the signal conditioning comparator.
5.2. Closed-loop Motor Control
Negative feedback generally promotes faster settling to an equilibrium condition and reduces the effects of perturbations, as opposed to positive feedback. Systems employing negative feedback loops, in which just the right amount of correction is applied with optimum timing, can be very stable, accurate, and responsive.
Considering the problem of controlling the speed of a DC motor, we will use negative feedback to cause the motor speed to be linearly dependent on the Analog Input Control voltage. Since the speed of the motor is roughly proportional to the applied voltage, it would seem that one would simply need to construct an equation that describes speed as that particular function of voltage, and then set the motor voltage based on the desired speed. This was the approach we took in Lab 6a. However, the motor speed is also a function of the load applied to the motor and dynamic effects such as friction and inertia. Closed-loop controllers are used to compensate for those issues that affect the motor speed and provide a linear response to linear inputs.
The issue now becomes choosing the algorithm that the microprocessor must implement to provide the desired speed control under varying load conditions. As described in Appendix C of Unit 6, classical controls uses proportional plus integral plus derivative (PID) control, which works well for controlling many dynamic systems. Other types of controllers use fuzzy logic and artificial neural networks (ANN) and are most suited for controlling extremely nonlinear systems.
Because of the difficulty of “tuning” PID controllers to avoid instability, this lab will use just proportional plus integral (PI) control. Classical control designs use mathematical equations to describe continuous systems and define the controller action, specifically differential equations and Laplace transforms. For digital computers to implement the controller action, the continuous equations must be transformed into a form that can be converted to digital code, as discussed in Unit 6.
6. Problem Statement
As illustrated in Fig. 5.1, closed-loop control incorporates a feedback signal along with the analog and discrete inputs to the control process. The tachometer frequency will be measured by using the Input Capture of the PIC32 to determine the signal period which is then inverted to yield the frequency. The tachometer period measurements are filtered with a moving averaging low pass digital filter as described in Lab 6a.
This lab is to use a digital implementation of proportional plus integral (PI) control in the control loop. The speed of the motor will be linearly dependent on the voltage controlled by the Analog Input Control potentiometer. This is described by Eq. 6.1 which results in linear motor speed control that will vary between 30% and 90% of maximum motor speed.
$$Motor Speed = \bigg[ \bigg( \frac{Analog Control Voltage * 0.6}{Maximum Analog Control Voltage} \bigg) + 0.3 \bigg] \cdot Maximum motor speed \qquad (Eq. 6.1)$$
The range of 30% to 90% is selected on the characteristics of the DC motor we are using for Lab 6a and 6b. By experimentation, it was determined that when the motor supply is set to 5.0 V, the %PWM must be set above 25% to 28% or the motor will not turn as shown in Fig. 8.3 of Lab 6a. If the motor is not turning, then there are no input capture interrupts to set the RPS variable in the control algorithm.
7. Background Information
7.1. Closing the Control Loop
Because of ease of implementation and stability, we will implement proportional plus integral (PI) control in this lab. The control algorithm for the PI control is implemented by the pseudo code of Listing 7.1. This code is executed at the frequency established by the PWM PERIOD. Any update to the PWM duty cycle is made when Timer 2 resets.
The software shown in Listing B.6 of Lab 6a specifies where to add the PI control code for the pseudo code in Listing 7.1 below. (This code is reproduced from Listing C.1 of the Unit 6 tutorial.) Using the motor specified in the Equipment List, the constant (KP+KI) is set to 60/1024 and (KP-KI) to 60/1024. These constants were selected by experimentation solely for demonstration purposes and may need to be adjusted for other types of motors.
Listing 7.1. Pseudo Code for Digital PI Controller
#define GetPeripheralClock() 10000000 // PBCLK set in config_bits.h
#define PWM_MAX (GetPeripheralClock()/10000) // Set output range
#define PWM_MIN 0
static int ERROR = 0; // Initial value for en-1
static int CTRL = 0; // Initial value for cnn-1
TACH = Read motor speed (Hz); // Global variable set by InputCapture ISR
// The SET_SPEED reference input is scales using a first order polynomial in the form y = ax + b to set the slope, a, with
// units rps/ADC bit and ”b” being the minimum speed when the ADC input is zero
SET_SPEED = Scaled potentiometer setting // Determine speed set point from ADC
ERROR_LAST = ERROR; // Save previous error and control values
CTRL_LAST = CTRL;
ERROR = SET_SPEED - TACH; // Compute new error value
CTRL = (KP + KI)*ERROR - (KP - KI)*ERROR_LAST + CTRL_LAST; // Compute new control output value
if(CTRL > PWM_MAX) then PWM_CONTROL = PWM_MAX; else // Limit output range to prevent windup
{
If (CTRL < PWM_MIN) then PWM_CONTROL = PWM_MIN; else
PWM_CONTROL = CTRL; // Output PWM value
}
Figure 7.1 was generated by monitoring the motor tachometer using the SPI_CK DIO 4 pin on the Analog Discovery 2 connector that is toggled in the input capture ISR, as shown in Listing B.4 of Lab 6a. Examining the plot for the tachometer in Fig. 7.1, we see than the PI algorithm requires about 150 ms to achieve steady state.
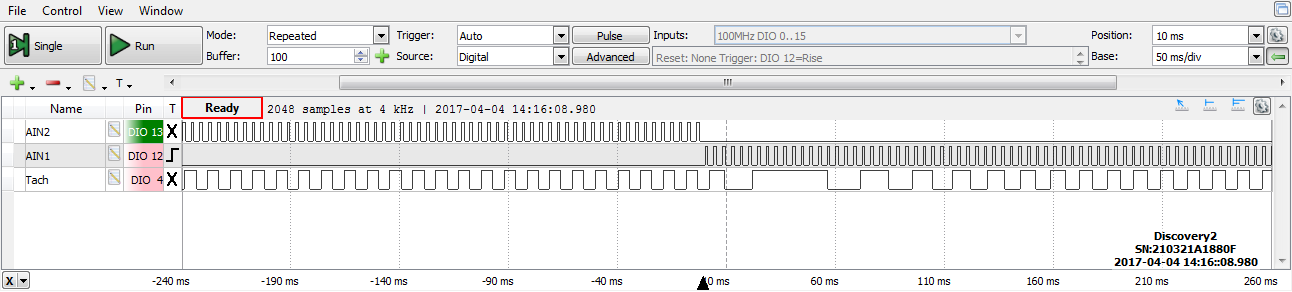 Figure 7.1. Motor speed response for a step input from CW to CCW at 30% PWM for PI closed-loop control.
Figure 7.1. Motor speed response for a step input from CW to CCW at 30% PWM for PI closed-loop control.
8. Lab 6b
The DC motor used in Lab 6a and 6b has a 19 to one reduction gear on the output shaft. The Hall Effect sensor used for the tachometer is mounted to the motor shaft and hence will be rotating 19 times faster than the output shaft. All motor speed measurements are based on the tachometer.
This lab will be divided into two phases. The first phase uses open-loop control with proportional control that includes the tachometer input to the processor. The tachometer input will be filtered with a moving average digital filter before being displayed on the LCD and sent to the UART.
Phase two incorporates proportional plus integral control of the motor speed control. The reference input, $r_n$, will be derived from the Analog Control Input using the relationship previously described in Eq. 6.1.
8.1. Requirements
- Phase 1: Background Tasks
- Same as background tasks for Lab 6a.
- Set peripheral bus clock for 10 MHz in config_bits.h.
- Timer 2 is to be used for the PWM generation
- Set the Timer 2 input clock for 10 MHZ
- Set the Timer 2 period for 10000 counts
- Timer 3 is to be used as the time reference for input capture.
- Set the Timer 3 input clock for 625000.
- Set the Timer 3 period for maximum counts (65536).
- Phase 1: Foreground Tasks
- Same as foreground tasks for Lab 6a.
- Basys MX3 JA-10 (PIC32MX370 Port G pin 9) is to be used for the Input Capture channel 1.
- Input Capture ISR
- An interrupt is to be generated on each positive transition of the tachometer signal.
- Read the captured Timer 3 value.
- Compute the period of the tachometer signal as the difference between two successive Timer 3 captures.
- Implement a fourth order Moving Averaging low-pass filter to reduce noise on the period measurement.
- Compute the motor speed in RPS to be used in the PI control loop and the background display tasks, assuming that the motor speed in revolutions per second (rps) is the same as the tachometer frequency.
- Timer 2 ISR
- Read the ADC
- Compute the set speed using Eq. 6.1 above
- Compute the actual motor speed as a percentage of maximum speed when PWM is set to 100%.
- Implement the control algorithm following the pseudo code shown in Listing 7.1 and using the control constants provided in Unit 6 background text.
- Phase 2: Background Tasks
- All background tasks are to be serviced every 250 ms.
- The motor speed setting (spd), the tachometer measurement (rps), PWM control output (cn), and the control error (en) is to be displayed on the Basys MX3 LCD as shown in Fig. 8.1.
- In addition to the data displayed on the LCD in Fig. 8.1, display the measured Analog Input Control voltage on your workstation terminal as shown in Fig. 8.2.
- Using the slide switches on the Basys MX3 board, control the motor operations as listed in Table 8.1.
- Phase 2: Foreground Tasks
- Input Capture ISR
- Compute the difference in Timer 3 ticks between two successive positive transitions of the tachometer.
- Implement a 4th order moving average on the tachometer period.
- Compute the motor speed in RPS.
- The Timer 2 will serve the following functions:
- The PIC32 ADC will read the digitized value of the “Analog Input Control” voltage.
- Scale the analog control voltage as described by Eq. 6.1.
- Compute the PWM output from the proportional plus integral (PI) algorithm.
- Write to the output compare secondary registers (OCxRS) that generate the PWM output.
 Figure 8.1. LCD display for closed loop operation.
Figure 8.1. LCD display for closed loop operation.
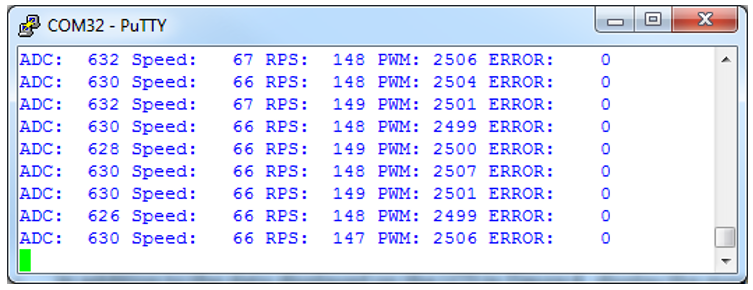 Figure 8.2. Terminal screen for closed loop motor control.
Figure 8.2. Terminal screen for closed loop motor control.
Table 8.1. Motor control modes.
| Slide Switch | LOW | HIGH |
|---|---|---|
| SW5 | Run the motor according to the direction set by SW7 | Coast operation |
| SW6 | Run the motor according to the direction set by SW7 | Brake (STOP) |
| SW7 | Rotate CCW at speed set by analog input control | Rotate CW at speed set by analog input control |
